GGU-2D-SSFLOW: Vertical-plane system and axis-symmetrical system
The program solves the differential equation:
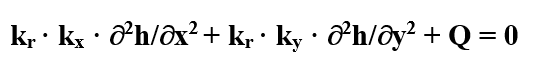
Where
kx, ky = Permeability in, e.g., m/s for x and y direction
h = Piezometric head in e.g. m
kr = Coefficient for determination of permeability in the unsaturated zone (dimensionless)
Q = Discharge in e.g. m³/s
x, y = Coordinates in e.g. m
The value kr records the change in permeability in the unsaturated zone r, above groundwater, and can take on values between 0.0 and 1.0. In the saturated area of the system kr is 1.0. The value kr is a function of the pore water pressure u. The pore water pressure u is calculated from the piezometric head h, the elevation head y and the unit weight of water w.
u = (h - y) · ![]() w
w
In Figure 4, the curves are presented for three typical soils. Using this value in the differential equation has the distinct advantage, for the following finite-element calculation, that phreatic lines can be very easily calculated.
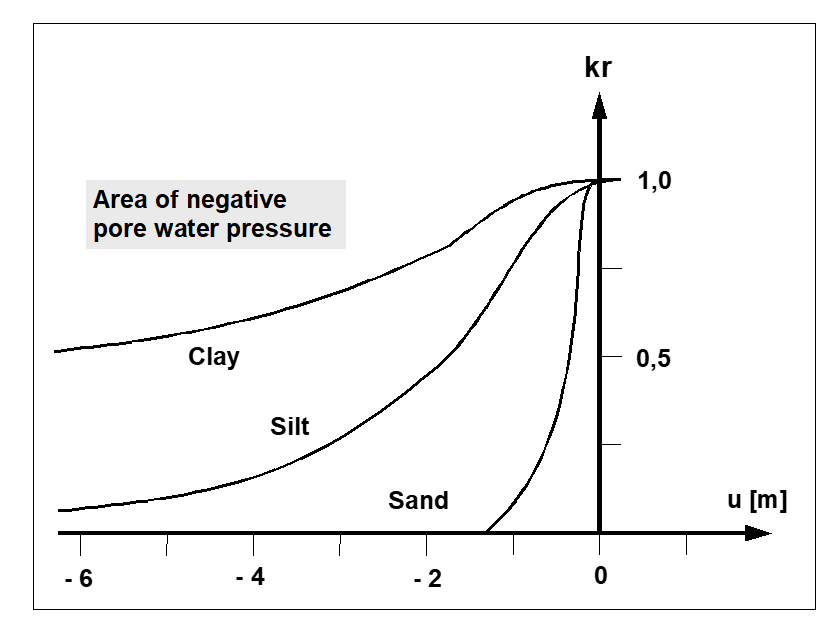
Figure 4 Function kr = f(u)
Figure 5 serves as a further explanation. For the case of a horizontal groundwater table, all four variables h, y, u and kr are given as functions.
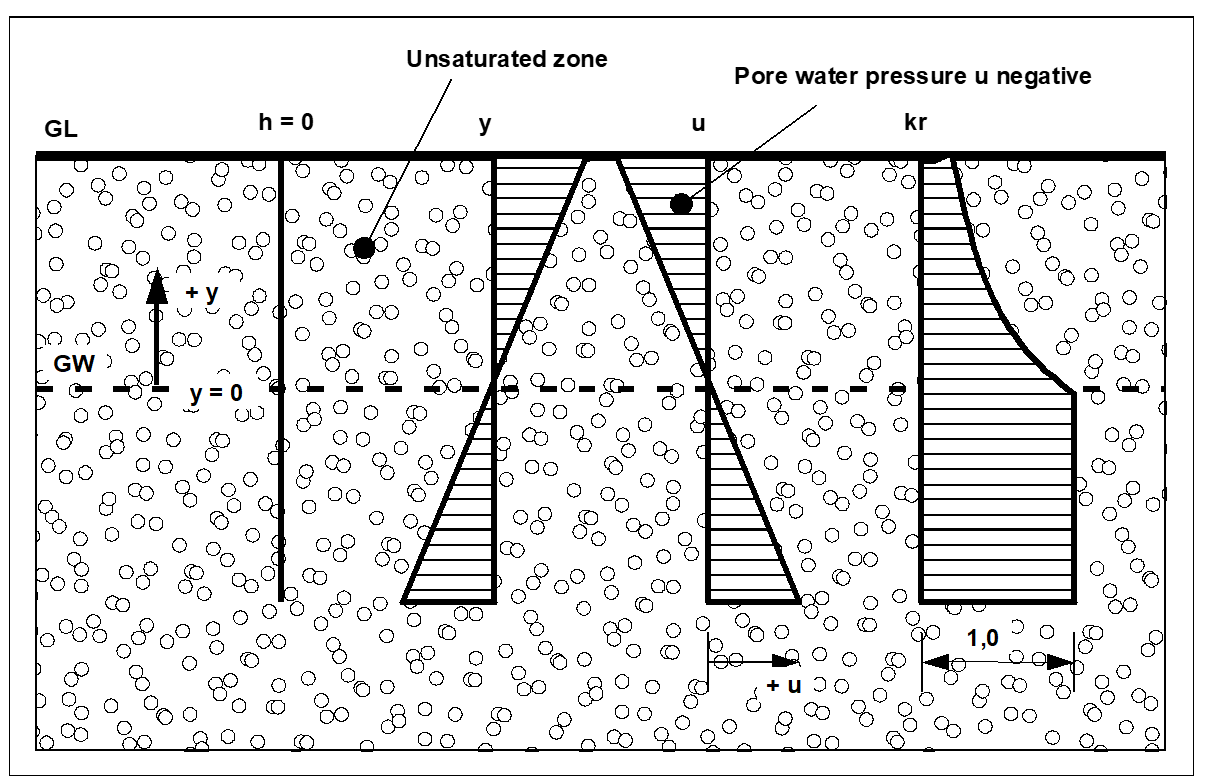
Figure 5 Unsaturated zone
If unsaturated zones are present in the system, and a phreatic line analysis is to be carried out, an iteration process is required, as the position of the phreatic line is not known from the outset. In the first iteration step, the program assumes that all areas of the system are saturated:
kr = 1.0.
After the initial calculation of the piezometric heads at the system nodes, the pore water pressures u are calculated and kr determined. With the altered permeabilities, a new calculation of the system follows, with new piezometric heads and correspondingly new pore water pressures and kr values. The iteration process is carried on until the difference in piezometric head in iteration step (i) and (i - 1) falls below the user-defined limit value (iteration divergence).
Note on boundary conditions:
The case of an impermeable boundary is automatically taken in to account by the finite-element-method. Valid is, that all system boundaries or partial system boundaries which have no water level or source boundary conditions, are automatically impermeable.
