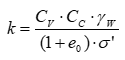GGU-CONSOLIDATE: Consolidation settlements for non-linear compression
This approach is based on a suggestion by Prof. Dr.-Ing. Hartmut Schulz. The explanatory text originates principally from Prof. Schulz.
In the following figure, this approach is demonstrated. Such representations are attained from the evaluation of load-settlement tests. The GGU-OEDOM program allows such representations and test evaluations.
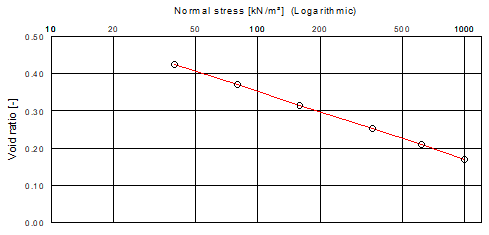
The initial assumption is of a linear reduction of the pore ratio e with the logarithm of the effective vertical stress σ'. From this, the compression is found by relating it to the total volume.
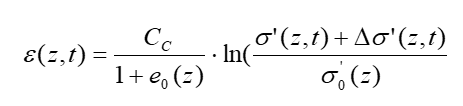
ε(z,t) = compression as a function of the location z and the time t
CC = compression index
e0(z) = pore ratio at z before loading
σ0'(z) = stress at z before load increase
Δσ0'(z,t) = compression change as a function of z and t
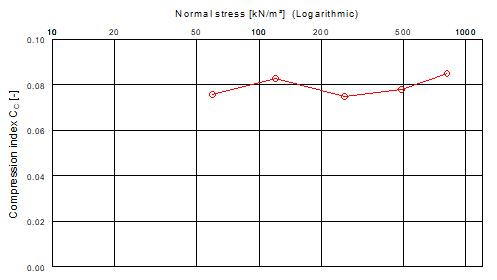
This equation already incorporates the fact that the effective vertical stresses are functions of the location z within the layer and the time t during the consolidation process. It is also taken into account that the pore ratio changes linearly with the logarithm of the change in stress. This means that the compression coefficient CC is a constant. The example in the figure above corresponds to the evaluation in the following figure (stress-compression coefficient relationship in the GGU-OEDOM program), which shows that in this case the compression coefficient CC is almost constant over the entire stress range (CC ≈ 0.08). Only then can calculations be carried out using this approach.
The following input values are required for each layer:
Compression index CC
Pore ratio e0(top) = pore ratio e0 at top of layer
Stress σ'0(top) = effective stress σ'0 at the top of the layer before loading
Stress σ'0(bottom) = effective stress σ'0 at the bottom of the layer before loading
The program first determines the pore water pressure distribution Δu(t,z) at time t across the layer depth z. The methods already explained in the previous sections are used for this purpose. The change in stress is then calculated:
Δσ'(z,t) = σ0'(z) + Δu(z,t)
σ0'(z) can be calculated from σ'0(top) and σ'0(bottom).
Further, the pore ratio e0(z) is computed from:
e0(z) = e0(top) + ln(σ'0(top)/ σ0'(z))·CC
We now have all variables to facilitate evaluation of the above equation.
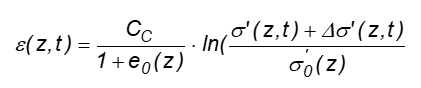
A dimensionless compression for the depth z is acquired for each time step. The integration of these values across the depth provides the settlement s(t).
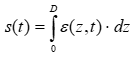
D = layer thickness
The equations described here are implemented in the program.
If you use the consolidation coefficient CV and the compression index CC in your calculations, the program also provides a permeability determined using: