GGU-CONSOLIDATE: Consolidation theory after Terzaghi and analytical solution
If cohesive layers are loaded faster than they can release their pore water, excess pore water pressures result, which are only gradually dissipated. This process is known as consolidation. Assuming the validity of Darcy's Law (v = k · i) and Hooke's Law (ε = σ'/Es), the following differential equation must be solved:
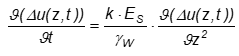
For the one-dimensional case with constant pore water pressure, a closed solution exists (see e.g. Grundbautaschenbuch 1990, Teil 3 - "Foundation Engineering Pocketbook 1990, Part 3" -, or Braya M. Das (1983); Advanced Soil Mechanics; McGraw Hill). The following input values are required:
Δu = excess pore water pressure (constant for the whole layer depth) = surcharge p
Es = constrained modulus of layer
k = permeability of layer
d = thickness of layer
t = time at which the excess pore water pressure is to be determined.
The program computes the consolidation coefficient CV from the constrained modulus and
permeability.
CV = Es · k / γw
Where
γw = 10 kN /m³ ≅ unit weight of water
In some cases, this value is known from load-settlement tests, making input of constrained modulus and permeability superfluous. Using the switch provided, you can define whether input is to be via constrained modulus + permeability or via consolidation coefficient CV.
Furthermore, the drainage conditions of the layer must be considered:
Draining to the top and bottom;
Draining to the top only;
Draining to the bottom only.
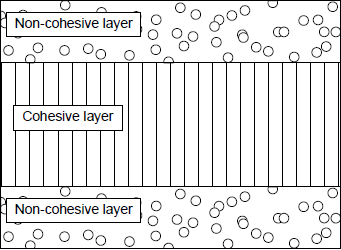
In the figure a consolidation layer is shown, which can drain to the top and bottom. The pore water pressure distribution is constant across the whole layer depth and corresponds to the surcharge load p, which can be defined within the program. The program models the pore water pressure distribution u across the layer depth in definable, constant, vertical steps, at user-defined times. The area of the pore water pressure distributions is numerically integrated. By comparing this with the constant pressure distribution in the unconsolidated state (t = 0), the degree of consolidation U can be determined. The following is valid:
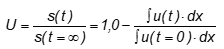
A further term is the consolidation ratio Uz, which is defined as:
Uz = 1,0 - u/um
where
u = pore water pressure
um = u / surcharge load
