GGU-CONSOLIDATE: Secondary settlements

Secondary settlements are the result of volume changes occurring under constant effective stresses. Current scientific knowledge indicates that the increase in settlement with time is independent of the size of the effective stresses. The volume changes can be mathematically described as follows (Garlanger, 1972):

Where:

e = void ratio,
e₉₈ = void ratio for a degree of consolidation of 98% (practical end of consolidation),
C_α = creep coefficient, relative to void ratio,
t = time from commencement of consolidation, t ≥ t₉₈,
t₉₈ = time for a degree of consolidation of 98%, from commencement of consolidation.

Secondary settlements are caused by viscous effects in the ground or porewater. The governing laws were first reported by Buisman, 1936, based on settlement observations:

where:

ε = compression,
ε₉₈ = compression for a degree of consolidation of 98%, (practical end of consolidation),
C_B = creep coefficient, relative to compression ,
t = time from commencement of consolidation, t ≥ t₉₈,
t₉₈ = time for a degree of consolidation of 98%, from commencement of consolidation.

It should be noted at this point that Equations (1) and (2) are used in the literature with both the natural and the decadal logarithm. In practice the decadal logarithm appears to be in more widespread use than the natural logarithm.

The secondary settlements relevant for practical purposes are given by Equation (2) by integration over the layer thickness:

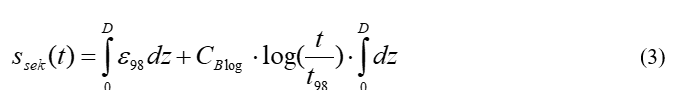
where:

s_sek(t) = secondary settlements as a function of time t,
z = depth coordinate [m],
D = original stratum depth [m],
C_Blog = creep coefficient, relative to compression ε and the decadal logarithm.
The conversion to the corresponding value for the natural logarithm:
C_Bln = 1/ ln 10 · C_Blog = 0,434 · C_Blog

If integration is performed and the entire settlement process is adopted as a function of time, the following expressions result:

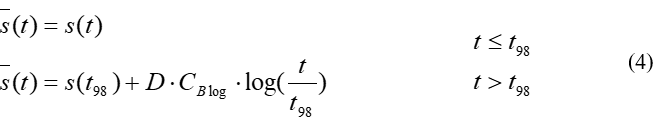
with the additional variables:

= secondary settlements as a function of time t [m],
s(t) = consolidation settlements as a function of time t [m],
s(t₉₈) = settlement as a result of consolidation and a degree of consolidation of 98% [m].

Strictly, secondary settlements commence together with consolidation settlements. They are allowed to begin later for analyses.

According to Kulhawy and Mayne, 1990, the ratio c_α/c_c may lie between 0.04 and 0.06 for organic soils: c_α can be interpreted as a compression index for secondary settlements and is a function of the compression index for primary settlements. If the mean value of this ratio is adopted it may be written as follows:

c_α (I_p) = 0,05 × c_c(I_p)  bzw.  c_α (w_L) = 0,05 × c_c(w_L)                 (11)

This relationship also applies if the compression index is represented as a function of the water content at the liquid limit. It gives the time-dependent secondary settlements by integrating the change in void ratio e over the layer thickness d:

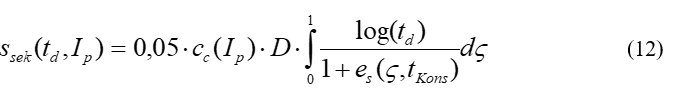
Rough numerical values (abstract from TUM handouts by Prof. Vogt):

The following empirical values may be adopted in terms of secondary settlements: C_α < 0.005 for overconsolidated clays, 0.005 < C_α < 0.05 for normally consolidated clays and 0.05 < C_α < 0.5 for organic and humous soils. Rheologically, soil creep is regarded as viscous behaviour.

If changes in relative settlements or vertical strains ε are described instead of the change in
void ratios, the Buisman factor C_B (BUISMAN, 1936) is adopted instead of the creep factor C_α. Where:

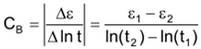
and C_α = C_B · (1 + e₀).

A relationship exists between the Buisman constant C_B and the compression index C_C for primary settlement via the toughness index l_v where C_B = C_C · I_v /(1 + e).

The toughness index I_v correlates well with the water content at the liquid limit w_L.

I_v [%] = -7.02 + 2.55 · ln (w_L [%]).

A relationship also exists between creep velocities (compression rates) ε, reference times t (theoretical time since load application), toughness index I_v and effective stresses σ' (KRIEG 2000):

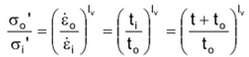
In this context it is obvious that the creep velocities can be reduced by reducing the effective loads and that compression rates are a function of both the stress levels and the time elapsed since the load was applied.

KRIEG, S. (2000): Viskoses Verhalten von Mudden, Seeton und Klei. Heft 150, Veröff. Inst. Bodenm. u. Felsm.
Univ. Karlsruhe

Further literature: