GGU-SLAB: Analysis using the constrained modulus method
The following analysis dialog box opens:
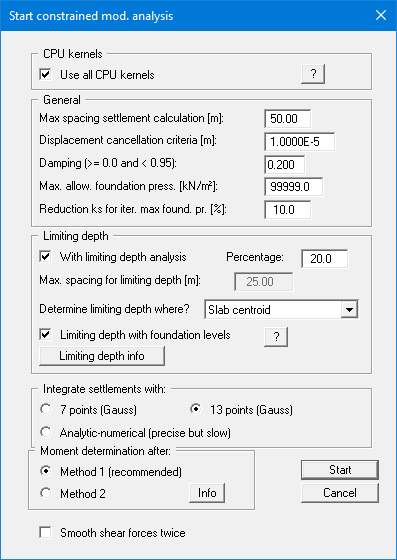
"CPU kernels" group box
The analysis according to the constrained modulus method can take a lot of time for more complex systems. If you activate this check box, all CPU kernels of your computer are used. This can considerably reduce the calculation time."General" group box
The following condition must be adhered to when using the constrained modulus method:
Deflection curve of slab = settlement depression of elastic-isotropic half-space
In contrast to the subgrade reaction modulus method the constrained modulus method therefore requires an iteration process. In the first step the settlements (elastic-isotropic half-space) at all FEM mesh nodes are calculated for a constant load of 1 kN/m² on the FEM elements. The settlement resulting from the triangle loads at every FEM mesh node must be determined for this. For example, a mesh comprising 512 triangles and 289 nodes requires
512 · 289 = 147,968 (!) settlement calculations.
In an attempt to limit the settlement analysis time the "Max. spacing settlement calculation" allows input of a spacing. The settlements at system nodes are only determined from triangles with their centroids at a smaller distance to the system node than is defined here.
The end of iteration is defined using "Cancellation criteria displacement". If the difference between the displacement of the slab and the calculated settlement (elastic-isotropic half-space) is smaller than the specified value at all points of the FEM mesh, the analysis is stopped.
The program recalculates the subgrade reaction moduli for the next iteration step from the quotients of the pressure at the node (ks · w) and the settlement (elastic-isotropic half-space) after every iteration step. In complicated systems this can lead to oscillations around the actual solution, the calculation does not converge. In this case, a "Damping" can be specified. The value 0.2 given in the dialog box has provided good results in the past. Values between 0.0 and 0.95 make the most sense. A value of 1.0 (complete damping) makes no sense and will therefore not be accepted by the program.
Theoretically infinitely high foundation pressures occur at the system boundaries when employing the constrained modulus method. This effect is reduced to stress peaks by use of finite analysis methods. If you need to avoid these stress peaks you may define a "Max. allowable foundation pressure". After every iteration step the program checks whether this maximum foundation pressure has been exceeded. If it is exceeded the subgrade reaction modulus is reduced before carrying on with the next iteration step. This is done by calculating the subgrade reaction modulus at the appropriate points not from:
ks · w/s
but instead by using:
ks = max. allow. foundation pressure/s
to calculate. Unfavourable numerical oscillations can also occur in the solution. You can therefore specify a maximum reduction of the subgrade reaction moduli at the appropriate locations so that a complete reduction is not immediately applied. Instead, the existing subgrade reaction modulus can be reduced by, for example, a maximum of 10% each time. Enter this percentage value in "Reduction ks for iter. Max. found. pr.".
"Limiting depth" group box
The limiting depth can be determined to DIN 4019. The "Percentage" defines the position of the limiting depth. The limiting depth is thus given by the condition:
Soil surcharge · percentage = stress below the triangle element
The limiting depth can be calculated at given points of the slab ("Slab centroid", "Arbitrary point") or for every triangle element ("Everywhere"). Further information on the methods used can be read by pressing the "Limiting depth info" button.
If foundation levels <> 0.0 are present, the "Limiting depth with foundation levels" can be determined. If you have deactivated the check box, limiting depth analysis is performed from ground level."Integrate settlements with:" group box
The settlement calculations for the elastic-isotropic half-space are performed using a Gaussian numerical integration. Integration using 7 points and 13 points is available. If you need higher precision (for slightly longer computation times) and are not superstitious, use integration with 13 points. The option of analytic-numerical determination of settlements is also provided. The analysis is precise, but takes a little longer."Moment determination after:" group box
With regard to the determination of moments, please see the description in the section on the subgrade reaction modulus method.
A cancellation window opens after analysis starts. If you press the "Cancel" button the analysis is not immediately aborted. You may first edit all the parameters described above and, if required, continue with the analysis.
An analysis using the constrained mod. method takes considerably longer than the subgrade reaction modulus method due to the extensive settlement calculations necessary.
