GGU-SLUGTEST: Program concept

For the type curve method the program employs published solutions in Laplace space for the differential equations used to describe the slug test. Using to the model adopted by COOPER et al. (1967) and C_D = ¹/₂ the solution for the dimensionless water level in Laplace space is:

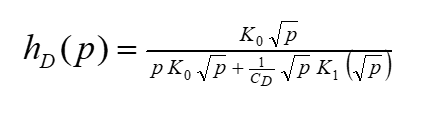
where:

h_D :  Laplace transform [-]

p :    Laplace variable [-]

C_D : Dimensionless wellbore storage [-]

K₀ :  Bessel function of the second kind, Order 0 [-]

K₁ :  Bessel function of the second kind, Order 1 [-]

The real solutions that can be derived from this can be calculated using analytical methods, but they require much more effort and often lead to unsatisfactory results. The Laplace transform is therefore inverted numerically by the GGU-SLUGTEST program.

The Laplace transform of a function h_D(t) is defined as:

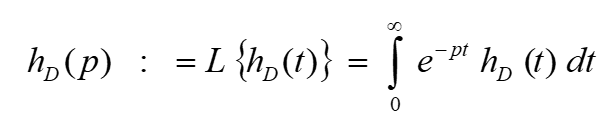
The numerical inversion can be formulated after STEHFEST (1970 a,b) as:

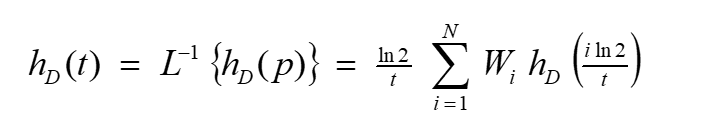
where:

N :  Even number [-]

W : Weighting factor [-]

In theory, h(t) is all the more precisely approximated the larger N is (STEHFEST, 1970 a). However, because the calculation precision depends on the number of digits processed by the computer used, rounding off errors increase with increasing N. N should therefore be selected in accordance with the precision of the computer.

The best results are obtained from the GGU-SLUGTEST program with N = 12 to N = 16, depending on the function to be inverted for the Laplace transform (dimensionless water level).

On this basis, you can use the GGU-SLUGTEST program to generate any type curves for evaluation of the implemented slug test models. Adjustment of the measured data to the type curves can then be carried out either in the conventional manner, i.e. by hand on the screen, or by an automatic fit. If required, a second fit routine even generates the optimum type curve for your data.