GGU-CONSOLIDATE: Sekundärsetzungen

Sekundärsetzungen resultieren aus Volumenänderungen, die unter konstanten effektiven Spannungen auftreten. Ihre zeitliche Zunahme ist nach derzeitigem Stand der Wissenschaft unabhängig vom Betrag der effektiven Spannungen. Mathematisch lassen sich die Volumenänderung wie folgt beschreiben (Garlanger, 1972):

Hierin sind:

e Porenzahl
e₉₈ Porenzahl bei einem Konsolidierungsgrad von 98 % (praktisch das Ende der Konsolidation)
Kriechbeiwert, bezogen auf die Porenzahl
t Zeit von Beginn der Konsolidation an gerechnet, t ≥ t₉₈
t₉₈ Zeit bei einem Konsolidierungsgrad von 98 %, ab Beginn der Konsolidation gerechnet

Grundlage der Sekundärsetzungen sind Zähigkeitseffekte des Bodens bzw. des Porenwassers, über deren Gesetzmäßigkeiten Buisman, 1936, unter Bezugnahme auf Setzungsbeobachtungen in folgender mathematischer Form erstmalig berichtete:

mit:

ε Zusammendrückung (Stauchung)
ε₉₈ Zusammendrückung bei einem Konsolidierungsgrad von 98 % (praktisch das Ende der Konsolidation)
C_B Kriechbeiwert, bezogen auf die Zusammendrückung ε
t Zeit von Beginn der Konsolidation an gerechnet, t ≥ t₉₈
t₉₈ Zeit bei einem Konsolidierungsgrad von 98 %, ab Beginn der Konsolidation gerechnet

Es sei an dieser Stelle angemerkt, dass die Gleichungen (1) und (2) in der Literatur sowohl mit dem natürlichen als auch mit dem dekadischen Logarithmus verwendet werden. In der Praxis scheint die Verwendung des dekadischen Logarithmus weiter verbreitet zu sein als die Verwendung des natürlichen Logarithmus.

Die für praktische Zwecke interessierenden Sekundärsetzungen ergeben sich aus Gleichung (2) durch Integration über die Schichtdicke:

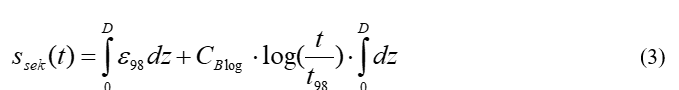
mit:

s_sek(t) Sekundärsetzungen als Funktion der Zeit t
z Ortskoordinate für die Tiefe [m]
D Ausgangsschichtdicke [m]
C_Blog Kriechbeiwert, bezogen auf die Zusammendrückung ε und auf den dekadischen Logarithmus.
Die Umrechnung auf den entsprechenden Wert für den natürlichen Logarithmus:
C_Bln = 1/ ln 10 · C_Blog = 0,434 · C_Blog

Führt man die Integration aus und bezieht man den gesamten Setzungsprozess als Funktion der Zeit in die Betrachtung ein, so ergeben sich die nachfolgenden Ausdrücke:

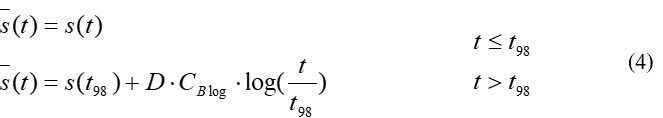
mit den zusätzlichen Größen:

  Sekundärsetzungen als Funktion der Zeit t [m]
s(t) Konsolidationssetzungen als Funktion der Zeit t [m]
s(t₉₈) Setzung infolge Konsolidation bei einem Konsolidierungsgrad von 98 % [m]

Streng genommen beginnen die Sekundärsetzungen bereits mit den Konsolidationssetzungen. Rechnerisch lässt man sie zu einem späteren Zeitpunkt beginnen.

Nach Kulhawy and Mayne, 1990, kann das Verhältnis c_α/c_c für organische Böden zwischen 0,04 und 0,06 liegen. c_α kann als Kompressionsbeiwert für sekundäre Setzungen interpretiert werden, der vom Betrag des Kompressionsbeiwert für primäre Setzungen abhängt und der, wenn der Mittelwert dieses Verhältnisses verwendet wird, wie folgt angeschrieben werden kann:

c_α (I_p) = 0,05 × c_c(I_p)  bzw.  c_α (w_L) = 0,05 × c_c(w_L)                 (11)

Dieser Zusammenhang gilt auch, wenn der Kompressionsbeiwert als Funktion des Wassergehalts an der Fließgrenze dargestellt wird. Aus ihm ergeben sich die zeitabhängigen Sekundärsetzungen durch Integration der Porenzahländerung e über die Schichtdicke d zu:

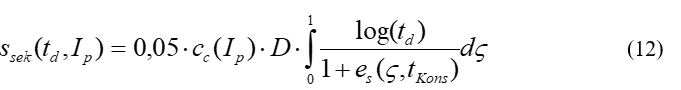
Weitere Literatur: