GGU-FOOTING: Theoretische Grundlagen für Kreis/Kreisring
Die Grundbruchsicherheit eines Kreises wird mit den Formeln in DIN 4017 berechnet.
Bei exzentrischer Laststellung muss eine Ersatzfläche A' bestimmt werden. Beim Rechteck ergibt sich die Ersatzfläche z.B. aus:
A' = (a - ex) · (b - ey)
mit: ex , ey = Exzentrizitäten
Die Ersatzfläche beim Kreis wird gemäß nachfolgender Abbildung (Leibnitz Universität, Hannover) berechnet:
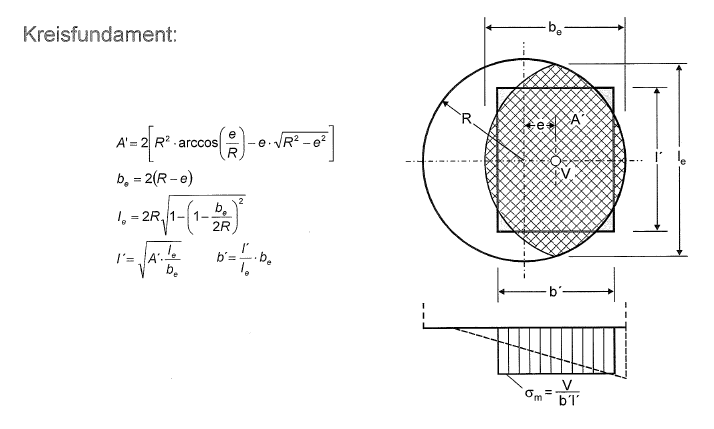
Weiterhin werden die 1. und 2. Kernweite benötigt. Für den Kreis gilt:
Kernweiten Kreis:
1. Kernweite = D / 8
2. Kernweite = 3 · π · D / 32
Für den Kreisring gibt es keine dem Kreis vergleichbaren Grundbruchformeln. Der Kreisring wird daher in einen äquivalenten Kreis umgewandelt. Die Umwandlung kann erfolgen über einen flächengleichen Kreis oder über einen Kreis mit gleichem Trägheitsmoment.
Kernweiten Kreisring:
1. Kernweite = [1 + (Di / Da)2] · Da / 8
2. Kernweite = 3 · π · Da / 32 · [1 - (Di / Da)4] / [1 - (Di / Da)3]
mit: Di = Durchmesser (innen)
Da = Durchmesser (außen)
Die Setzungsberechnungen erfolgen über dreiecksförmige Lastflächen, mit denen die Belastung von Kreis und Kreisring exakt nachgebildet werden kann [Dr.-Ing. Johann Buß, Setzungen und Spannungen unter "Dreiecksfundamenten", Geotechnik 22 (1999) Nr. 1].
Für Setzungsberechnungen wird die Lage des kennzeichnenden Punkts benötigt. Für den Kreis gilt:
Kennzeichnender Punkt Kreis = 0.845 · R
Für den Kreisring gibt es keine Herleitung des kennzeichnenden Punktes. Auf der sicheren Seite liegend wird mit der gleichen Lage des kennzeichnenden Punktes wie beim Kreis gerechnet:
Kennzeichnender Punkt Kreisring ⇒ Annahme = Kreis = 0.845 · Ra
mit: Ra = äußerer Radius
