GGU-LATPILE: Theorie 2. Ordnung
In GGU-LATPILE erfolgt die Berechnung von knickgefährdeten Pfählen nach den Vorgaben in der DIN EN 1993-1-1 .
Die Differentialgleichung für den normalen Biegestab lautet:
EI w''''(x) = q(x)
Beim sogenannten Knickstab wird die Normalkraft N berücksichtigt:
EI w''''(x) + N w''(x) = q(x)
Der Vollständigkeit halber ist hier die Differentialgleichung für ein zusätzlich gebettetes System dargestellt, da das Programm auch die parallele Bearbeitung von Systemen mit Theorie 2. Ordnung und elastischer Bettung zulässt. Die Formel lautet:
EI w''''(x) + N w''(x) + ks w(x) = q(x)
Die Berechnung erfolgt am verformten System. Nach
DIN EN 1993-5
Bemessung und Konstruktion von Stahlbauten,
Teil 5: Pfähle und Spundwände
wird die Berechnung von knickgefährdeten Pfählen nach der Theorie 2. Ordnung empfohlen und auf die
DIN EN 1993-1-1
Bemessung und Konstruktion von Stahlbauten,
Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau
verwiesen. Die Berechnung nach der Theorie 2. Ordnung liefert genauere Ergebnisse als die üblichen und vereinfachenden Ersatzstabverfahren.
Die Berechnung nach der Theorie 2. Ordnung erfordert eine Vorverformung bzw. Vorkrümmung des Grundsystems. Werte für die Vorkrümmung sind in Tabelle 5.1 in DIN EN 1993-1-1 enthalten.
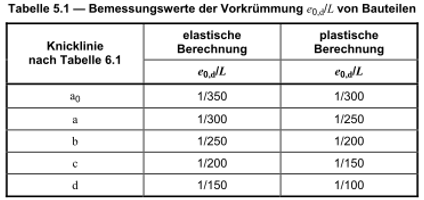
In Abhängigkeit von der Knicklinie werden Vorkrümmungen genannt. Vereinfacht kann bei Pfählen mit einer Vorkrümmung von e0,d/L = 1/150 gerechnet werden.
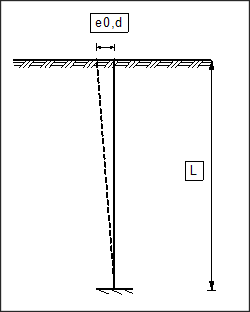
Bei eingespannten Pfählen ohne zusätzliche Weg-Randbedingungen ergibt sich das verformte System aus einer Schrägstellung des Pfahls wie in der folgenden Abbildung dargestellt.
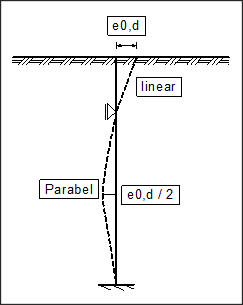
Bei Pfählen mit einer horizontalen Weg-Randbedingung (wx = 0) ergibt sich das verformte System aus einer linearen Vorkrümmung vom Auflagerpunkt bis zum Pfahlkopf und einer parabelförmigen Vorkrümmung zwischen den Auflagerpunkten und dem Pfahlfuß (siehe nachfolgende Abbildung).
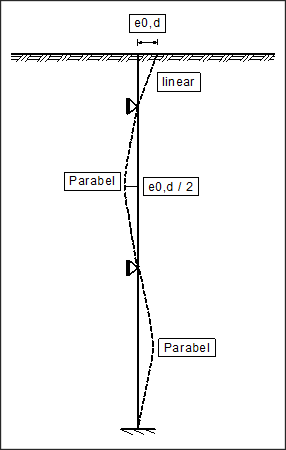
Die Länge L ergibt sich feldweise. Bei zwei Weg-Randbedingungen wird wie in der nachfolgenden Abbildung verfahren.
Die Einstellungen zur Theorie 2. Ordnung nehmen Sie im Berechnungsmenü "System / berechnen" vor.
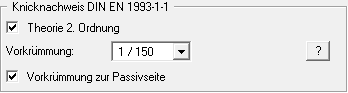
Hier kann die Größe der Vorkrümmung und die Richtung der Vorkrümmung vorgegeben werden. Es ist systemabhängig, ob eine Vorkrümmung zur Passivseite oder eine Vorkrümmung zur Aktivseite die ungünstigeren Bemessungswerte liefert. Deshalb erhalten Sie nach dem Berechnungsstart folgenden Hinweis:
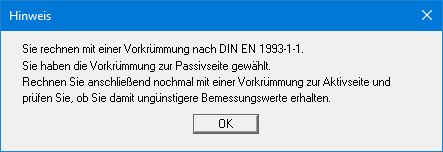
Sie müssen daher nach einer erfolgreichen Berechnung den Schalter "Vorkrümmung zur Passivseite" deaktivieren und mit einer erneuten Berechnung prüfen, ob mit einer Vorkrümmung zur Aktivseite schlechtere Werte erhalten werden.
Bei der Berechnung nach der Theorie 2. Ordnung erfolgt der erforderliche Iterationsprozess hinsichtlich der Verschiebung mit der Bemessungsnormalkraft Nd.
Die abschließende Bemessung erfolgt mit einem Spannungsvergleich:
σd ≤ fy,k / γM = fy,k / 1,1 = fy,d
Im Beispiele-Ordner sind 4 Dateien enthalten, die die klassischen Eulerfälle 1 bis 4 behandeln. Wenn Sie in den Systemdaten die Vertikallast V am Pfahlkopf geringfügig erhöhen und das System berechnen, erhalten Sie folgende Fehlermeldung:
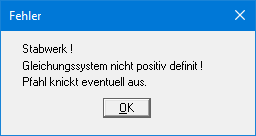
Die in den Dateien eingegebene Normalkraft entspricht somit der nach Euler ermittelten Knickkraft.
