GGU-SLAB: Berechnung mit dem Steifemodulverfahren

Sie erhalten folgende Dialogbox zur Berechnung:

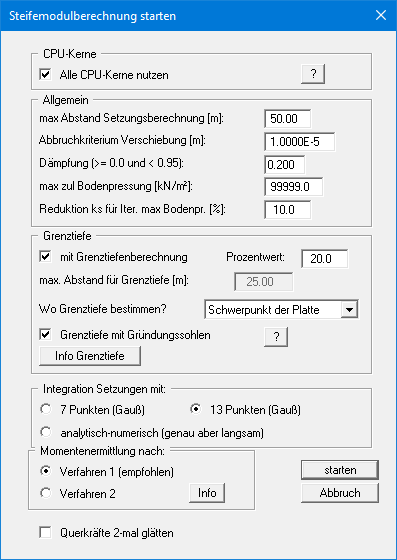
• Bereich "CPU-Kerne":
  Die Berechnung nach dem Steifemodulverfahren kann bei komplexeren Systemen viel Zeit in Anspruch nehmen. Wenn Sie diesen Schalter aktivieren, werden alle CPU-Kerne Ihres Rechners genutzt. Die Rechenzeit kann dadurch erheblich verkürzt werden.

• Bereich "Allgemein":
  Beim Steifemodulverfahren muss folgende Bedingung eingehalten werden:

Biegelinie der Platte = Setzungsmulde des elastisch isotropen Halbraums

Im Gegensatz zum Bettungsmodulverfahren erfordert das Steifemodulverfahren daher einen Iterationsprozess. Im ersten Schritt werden die Setzungen (elastisch isotroper Halbraum) an allen FE-Netzknoten infolge einer konstanten Belastung von 1 kN/m² auf den FE-Elementen berechnet. Dazu muss für jeden FE-Netzknoten die Setzung bestimmt werden, die sich aus der dreiecksförmigen Belastung der Dreiecke ergibt. Bei einem Netz mit z.B. 512 Dreiecken und 289 Knoten sind somit

512 · 289 = 147.968 (!) Setzungsberechnungen

erforderlich. Um den Rechenaufwand für die Setzungsberechnung eventuell zu begrenzen, kann mit dem Eintrag "max Abstand Setzungsberechnung" ein Abstand eingegeben werden, der bewirkt, dass Setzungen am Systemknoten nur aus Dreiecken bestimmt werden, deren Schwerpunkte einen kleineren Abstand zu diesem Systemknoten aufweisen.

Mit dem "Abbruchkriterium Verschiebung" definieren Sie das Ende der Iteration. Wenn an allen Punkten des FE-Netzes die Differenz zwischen der Verschiebung der Platte und der berechneten Setzung (elastisch isotroper Halbraum) kleiner ist als der angegebene Wert, wird die Berechnung beendet.

Das Programm berechnet die Bettungsmodule für den nächsten Iterationsschritt aus dem Quotienten aus Pressung am Knoten (k_s · w) und Setzung (elastisch isotroper Halbraum) nach jedem Iterationsschritt neu. Bei komplizierten Systemen kann das zu Schwingungen um die tatsächliche Lösung führen, die Berechnung konvergiert nicht. In diesem Fall können Sie eine "Dämpfung" vorgeben. Mit dem in der Dialogbox angegebenen Wert von 0,2 wurden gute Erfahrungen gemacht. Sinnvoll sind Werte zwischen 0.0 und 0.95. Ein Wert von 1.0 (volle Dämpfung) ist unsinnig und wird daher vom Programm nicht akzeptiert.

Beim Steifemodulverfahren treten an den Systemrändern theoretisch unendlich hohe Bodenpressungen auf. Durch finite Berechnungsmethoden wird dieser Effekt auf Spannungsspitzen reduziert. Falls Sie entsprechende Spannungsspitzen verhindern wollen, können Sie eine "maximal zulässige Bodenpressung" definieren. Das Programm prüft dann nach jedem Iterationsschritt die Bodenpressungen auf diesen Maximalwert. Falls eine Überschreitung festgestellt wird, wird an dieser Stelle vor dem Starten des nächsten Iterationsschritts der Bettungsmodul reduziert. Das geschieht in der Form, dass an entsprechenden Punkten der Bettungsmodul nicht aus

k_s · w / s

sondern aus

k_s = max zul Bodenpressung / s

berechnet wird. Auch dabei können ungünstige numerische Schwingungen der Lösung auftreten. Daher können Sie eine maximale Reduktion der Bettungsmodule an entsprechenden Stellen vorgeben, so dass nicht gleich in voller Größe abgemindert wird, sondern z.B. der vorhandene Bettungsmodul jeweils nur um maximal 10% reduziert wird. Geben Sie diesen Prozentwert unter "Reduktion ks für Iter. max Bodenpr. [%]" ein.

• Bereich "Grenztiefe":
  Die Grenztiefe kann in Anlehnung an DIN 4019 bestimmt werden. Mit "Prozentwert" definieren Sie die Lage der Grenztiefe. Die Grenztiefe ergibt sich damit aus der Bedingung:

Bodenauflast · Prozentwert = Spannung unter dem Dreieckselement

Sie können die Grenztiefe an bestimmten Punkten der Platte ("Schwerpunkt der Platte", "Beliebiger Punkt") oder für jedes Dreieckselement ("Überall") berechnen lassen. Weitere Informationen zu den Methoden erhalten Sie über den Knopf "Info Grenztiefe".

Wenn Gründungssohlen <> 0.0 vorliegen, kann die "Grenztiefe mit Gründungssohlen" bestimmt werden. Wenn Sie den Schalter deaktiviert haben, erfolgt die Grenztiefenberechnung ab OK Gelände.

• Bereich "Integration Setzungen mit:"
  Die Setzungsberechnungen für den elastisch isotropen Halbraum werden über eine numerische Integration nach Gauß durchgeführt. Es wird eine Integration mit 7 Stützstellen (Punkten) und mit 13 Stützstellen angeboten. Wenn Sie höhere Genauigkeit (bei etwas längerer Rechenzeit) wünschen und nicht abergläubisch sind, wählen Sie die Integration mit 13 Punkten. Es besteht aber auch die Möglichkeit, die Setzungen analytisch-numerisch zu ermitteln. Die Berechnung ist zwar genau, dauert dafür aber etwas länger.

• Bereich "Momentenermittlung nach:"
  Hinsichtlich der Momentenermittlung wird auf die Erläuterungen zum Bettungsmodulverfahren verwiesen.