GGU-SLUGTEST: Grundlegende Differentialgleichung
Mathematisch exakt wurde der Slug-Test erstmalig von COOPER et al. (1967) auf der Grundlage der Differentialgleichung für instationäre, radialsymmetrische Anströmung in einem gespannten, homogenen und isotropen Aquifer hergeleitet. Sie berücksichtigten dabei als eine wesentliche Randbedingung den endlichen Brunnenradius und damit die Eigenkapazität (Brunnenspeicherung) des Brunnens.
Der Ansatz lautet:
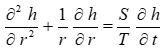
mit:
h : Höhe des Druckwasserspiegels [m]
r : Radiale Entfernung vom Brunnen [m]
t : Zeit [s]
T : Transmissivität [m²/s]
S : Speicherkoeffizient [-]
Die Differentialgleichung wird aus der Kombination des Massenerhaltungsgesetzes, dem Darcy'schen Gesetz und optional einer Zustandsbeschreibung hergeleitet (MATTHEWS & RUSSEL, 1967). Dabei wird konstantes radiales Fließen, ein gespanntes, homogenes und isotropes Medium unendlicher Ausdehnung sowie eine einzige Flüssigkeitsphase mit geringer und konstanter Kompressibilität vorausgesetzt.
Die Transmissivität gibt dabei an, welcher Volumenstrom einer Flüssigkeit mit einer definierten Viskosität unter einem hydraulischen Gradienten von 1 durch einen 1 m breiten Querschnitt eines Aquifers fließt, der die gesamte Mächtigkeit (m) des Aquifers umfasst und senkrecht zur Strömungsrichtung angeordnet ist (LANGGUT & VOIGT, 1980).
Damit besteht zwischen der Transmissivität und der Durchlässigkeit (kf) die Beziehung:
T = kf · m
Der Speicherkoeffizient ist eine Kenngröße für diejenige Wassermenge, die pro Oberflächeneinheit eines Aquifers bei der Änderung des Wasserspiegels um eine Einheit im Aquifer gespeichert oder daraus entlassen wird (KRUSEMANN & DE RIDDER, 1973). Der Speicherkoeffizient gilt in strengem Sinne nur für gespannte Aquifere und hängt von der Elastizität (bzw. Kompressibilität) des Korngerüstes und der Flüssigkeit ab. Das Volumen der Einzelkörner wird dabei als konstant betrachtet, da ihre Kompressibilität wesentlich kleiner als die des Korngerüstes und kleiner als die der Flüssigkeit ist (MATTHESS & UBELL, 1983, p. 159). Damit kann der Speicherkoeffizient definiert werden als (KRUSEMANN & DE RIDDER, 1990):
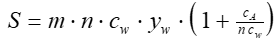
mit:
S : Speicherkoeffizient [-]
m : Mächtigkeit des Aquifers [m]
n : Porosität des Aquifers [-]
cw : Kompressibilität der Flüssigkeit [m²/N]
cA : Kompressibilität des Aquifers [m²/N]
γw : Wichte der Flüssigkeit [N/m³]
