GGU-STABILITY: ​Allgemeines zur Berechnung mit Faserkohäsion

Nichtbodenähnliche Abfälle wie z.B. unbehandelter Restmüll unterscheiden sich in ihrem Scherverhalten deutlich von Boden und bodenähnlichen Abfällen (Erdaushub, abgesiebte MBA-Fraktionen). Die Deutsche Gesellschaft für Geotechnik empfiehlt in ihren GDA-Empfehlungen entsprechend dieser Klassifizierung unterschiedliche Berechnungsverfahren. Nichtbodenähnliche Abfälle führen bei üblicher Einbautechnik zu geschichteten, anisotropen Deponiekörpern. Die Standsicherheitsberechnung für anisotrope Deponiekörper wird in der GDA-Empfehlung E 2-29 behandelt.

Nichtbodenähnliche Abfälle werden in abfallmechanischer Hinsicht in Anlehnung an die Grundsätze faserbewehrter Böden als Kompositmaterial, bestehend aus einer Grundmatrix und einer Fasermatrix, betrachtet. Nach der Modellvorstellung über das Zusammenwirken von Zug- und Reibungskräften in einem Kompositmaterial ergibt die Überlagerung der beiden Scherfestigkeitskomponenten i. A. eine nichtlineare Bruchbedingung. Derartige Bruchbedingungen sind von bewehrten Erdkörpern bekannt (EBGEO). Ursache der Nichtlinearität ist die begrenzte Normalspannungsabhängigkeit der Bewehrungswirkung.

Die Größe der aufnehmbaren Zugkräfte hängt von den Eigenschaften der Fasern und der Kornmatrix sowie von der Auflast ab. Die Festigkeitseigenschaften der Fasermatrix werden durch zwei Materialkennwerte beschrieben:

• die faserspezifische Zugfestigkeit z_max

• den Winkel ζ

Dazu kann ein auflastunabhängiger Anteil der Zugfestigkeit (z₀) kommen, der von einer Kohäsion c der Grundmatrix nicht unterschieden werden kann. Der Winkel ζ beschreibt die Normalspannungsabhängigkeit der Bewehrungswirkung. Die Aufnahme der Zugkräfte durch die Fasern ist begrenzt durch die faserspezifische Zugfestigkeit z_max. Bei Erreichen der faserspezifischen Zugfestigkeit reißen die Fasern, die Tragwirkung der Fasermatrix versagt.

Für die Ermittlung der Scherfestigkeit des anisotropen Abfallkörpers werden die Scherfestigkeitsanteile der Grund- und der Fasermatrix bestimmt. Dann werden die beiden Komponenten in der Berechnung überlagert. Aus den Zugkräften in den Fasern wird die so genannte Faserkohäsion τ(z) berechnet. Eine Besonderheit faser- und folienhaltiger, nichtbodenähnlicher Abfälle besteht darin, dass beim Dünnschichteinbau durch das Überfahren mit dem Kompaktor das Material plattgedrückt und horizontal ausgerichtet wird. Daraus ergibt sich das anisotrope Festigkeitsverhalten. Die Aktivierung der Faserkohäsion τ(z) hängt vom Winkel ϑ zwischen Faserlage und Scherfuge ab.

Mit den nach Grund- und Fasermatrix unterschiedenen Materialkennwerten (φ_GM, c_GM, ζ, z_max) können Standsicherheitsberechnungen durchgeführt werden. Durch den getrennten Ansatz kann einerseits die Anisotropie der Fasermatrix rechnerisch berücksichtigt werden, andererseits kann trotz der nichtlinearen Bruchbedingung mit auflastunabhängigen Materialkennwerten gearbeitet werden. Grundlage der Böschungsbruchberechnungen ist das Lamellenverfahren (DIN 4084:2002-11). Die Formel für die Berechnung der Lamellensohlkraft wird um einen Term für die vom Winkel ϑ abhängige Faserkohäsion erweitert. Die Lamellensohlkraft T berechnet sich zu:

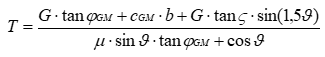
Dabei wird die folgende Bedingung eingehalten:

G / b · tan ζ < z_max

Beim Ansatz der Kohäsion c_GM ist zu berücksichtigen, dass auflastunabhängige Anteile der Scherfestigkeit sowohl bei der Grundmatrix (Kohäsion c_GM), als auch bei der Fasermatrix (auflastunabhängige Faserkohäsion τ(z₀) aus den auflastunabhängigen Zugspannungen) auftreten können. Da diese auflastunabhängigen Scherfestigkeitsanteile nicht exakt unterschieden werden können, dürfen diese nicht gleichzeitig in der Berechnung angesetzt werden.

Neben der Erweiterung der Formel zur Berechnung der Lamellensohlkraft wurden an den dem Programm zugrunde liegenden Berechnungsverfahren keine Änderungen vorgenommen. Es gelten die Ausführungen aus den “Theoretischen Grundlagen: Allgemeines zu Janbu und Bishop".

Die Eingabe der Bodenkennwerte ist in "Beispiel 2 - Dateneingabe von Hand” in “Schritt 2: Systemdaten eingeben (Bsp. 2) / Bodenkennwerte" für die konventionelle Berechnung ohne Faserkohäsion beispielhaft erläutert. Bei der Berechnung mit Faserkohäsion werden wie oben beschrieben weitere Kennwerte benötigt, die in die entsprechende Eingabemaske der Bodenkennwerte einzugeben sind (Beispiele nach GDA-Empfehlung E 2-35 und Collins et al., 1997).

Der Kennwert Aktivierungsgrad beschreibt das Verbundverhalten bei der Umsetzung der Zugkräfte in die Faserkohäsion. Neben der Verbundwirkung werden auch Effekte der Faserumlagerung u. ä. global berücksichtigt. Bei gutem Verbund (homogene Durchmischung von Grund- und Fasermatrix, reibungsstarke Grundmatrix usw.) kann der Aktivierungsgrad 1 betragen. Da es nur begrenzte Kenntnisse zum Verbundverhalten gibt, wird ein zurückhaltender Aktivierungsgrad von 0,7 empfohlen (Kölsch, 1996). In der Berechnung wirkt sich der Aktivierungsgrad wie ein zusätzlicher Teilsicherheitsbeiwert auf die Faserkohäsion aus.