GGU-3D-SSFLOW: Differentialgleichung
Das Programm löst die Differentialgleichung:
kr · kx · ![]() 2h/
2h/![]() x2 + kr · ky ·
x2 + kr · ky · ![]() 2h/
2h/![]() y2 + kr · kz ·
y2 + kr · kz · ![]() 2h/
2h/![]() z2 + Q = 0
z2 + Q = 0
Darin bedeuten
kx, ky, kz = Durchlässigkeit in z.B. m/s für x-, y- und z-Richtung
h = Standrohrspiegelhöhe in z.B. m
kr = Beiwert zur Bestimmung der Durchlässigkeit im ungesättigten Bereich (dimensionslos)
Q = Wassermenge in z.B. m³/s
x, y, z = Koordinaten in z.B. m.
Der Wert kr erfasst die Veränderung der Durchlässigkeit in der ungesättigten Zone r oberhalb des Grundwasserspiegels und kann zwischen 0.0 und 1.0 liegen. In gesättigten Systembereichen ist kr = 1.0. Der Wert kr ist eine Funktion des Porenwasserdrucks u. Der Porenwasserdruck u berechnet sich aus der Standrohrspiegelhöhe h, der Ortshöhe z und der Wichte des Wassers w.
u = (h - z) · ![]() w
w
In Abbildung 4 sind für drei typische Böden die entsprechenden Verläufe dargestellt. Die Einbeziehung dieses Wertes in die Differentialgleichung hat bei der späteren Finite-Element-Berechnung unter anderem den wesentlichen Vorteil, dass Sickerlinien sehr einfach berechnet werden können.
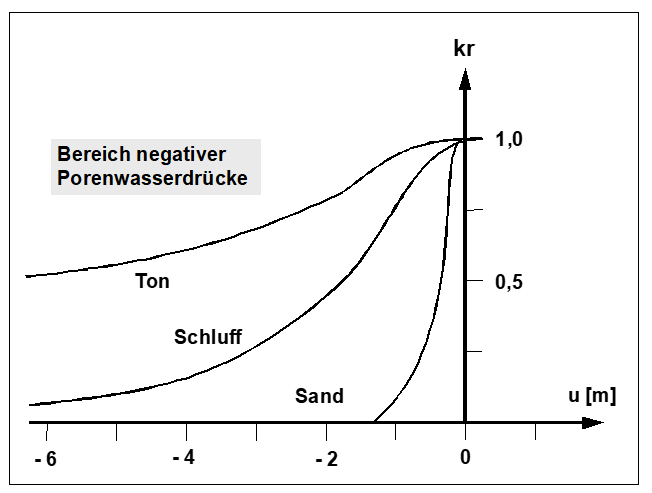
Abbildung Funktion kr = f(u)
Zur weiteren Erläuterung dient die folgende Abbildung. Für den Fall eines waagerechten Grundwasserspiegels sind alle vier Größen h, y, u und kr als Funktion aufgetragen.
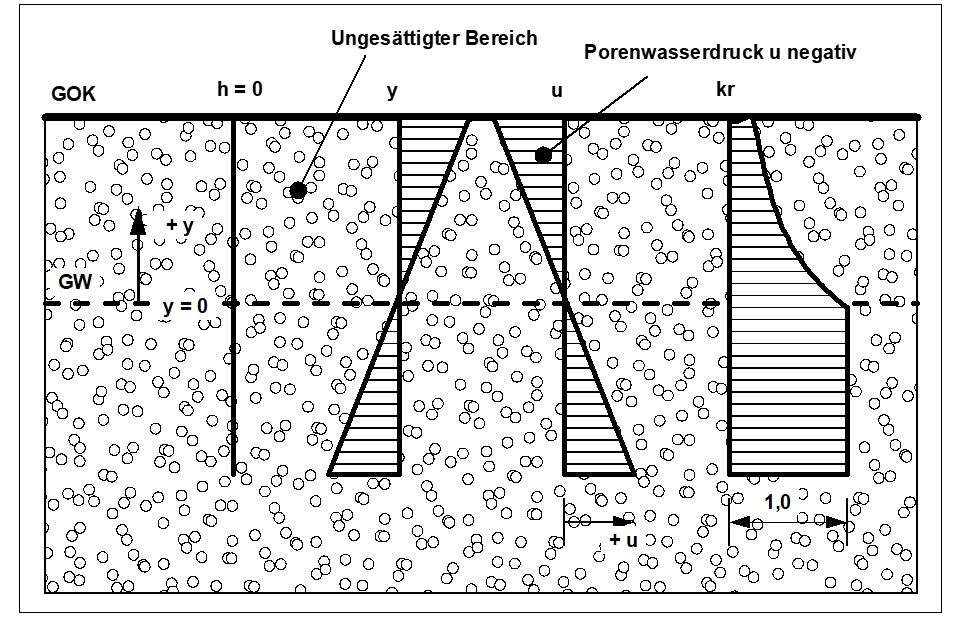
Abbildung Ungesättigter Bereich
Sind im System ungesättigte Bereiche vorhanden, und soll eine Sickerlinienberechnung durchgeführt werden, so erfordert das einen Iterationsprozess, da die Lage der Sickerlinie ja nicht von vornherein bekannt ist. Das Programm geht zunächst im ersten Iterationsschritt davon aus, dass alle Systembereiche gesättigt sind:
kr = 1.0
Nach der ersten Berechnung der Standrohrspiegelhöhen in den Systemknoten werden überall die Porenwasserdrücke u berechnet und der Wert kr bestimmt. Mit den so veränderten Durchlässigkeiten erfolgt daraufhin eine erneute Berechnung des Systems mit neuen Standrohrspiegelhöhen und entsprechend auch neuen Porenwasserdrücken und kr -Werten. Der Iterationsprozess wird so lange fortgesetzt, bis die Differenz der Standrohrspiegelhöhen im Iterationsschritt (i) und (i - 1) den vom Anwender vorzugebenden Grenzwert (Iterationsabweichung) unterschreitet.
Anmerkung zu Randbedingungen:
Der Fall einer undurchlässigen Berandung wird von der Finiten-Element-Methode automatisch berücksichtigt. Es gilt, dass alle Systemränder oder Systemteilränder, die keine Wasserstands- oder Quellen-Randbedingungen besitzen, automatisch undurchlässig sind.
