GGU-SLAB: Bettungsmodulverfahren

Das Programm löst die Differentialgleichung:

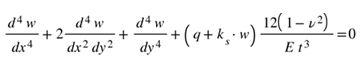
Darin bedeuten

w = Durchbiegung der Platte [m]

x, y = Koordinaten [m]

k_s = Bettungsmodul [kN/m³]

q = Flächenlast [kN/m²]

ν = Querkontraktionszahl der Platte [-]

E = Elastizitätsmodul [kN/m²]

t = Dicke der Platte [m]

Analytische Lösungen für diese Differentialgleichung existieren nur für einige wenige Sonderfälle, so dass bei Problemen der täglichen Bemessungspraxis (mit unterschiedlich verteilten Belastungen, freien, eingespannten oder gelagerten Rändern usw.) auf numerische Verfahren zurückgegriffen werden muss.

Die Differentialgleichung wird vom Programm mit der Finite-Element-Methode gelöst. Dabei werden Dreieckselemente verwendet. Für diese Dreieckselemente werden einfache Ansätze hinsichtlich der Verschiebung gewählt. Im vorliegenden Fall wird ein Verschiebungsansatz eingesetzt, der in Zienkiewicz (Carl-Hanser-Verlag, 1984, Seite 236) beschrieben ist. Dieser Verschiebungsansatz schneidet im Vergleich zu anderen Ansätzen sehr gut ab. Der gewählte Ansatz führt auf Gleichungssysteme, deren Anzahl Unbekannter der dreifachen Anzahl der Systemknoten entspricht. Die Gesamtlösung ergibt sich dann aus der mosaikartigen Zusammensetzung der Teillösungen über die Dreieckselemente. Es ist klar, dass mit zunehmender Verfeinerung des Finite-Element-Netzes die Qualität der Lösung gesteigert wird.

Die Momentenverteilung wird durch zweimalige numerische Differentiation der Biegefläche gewonnen. Durch eine numerische Differentiation wird immer ein Aufrauhungseffekt erzielt, der nicht gewünscht ist. Um das auszugleichen, bietet das Programm für die Momenten-Ermittlung zwei unterschiedliche Verfahren an:

• Verfahren 1:
  Die Momente werden in der Nachlaufrechnung in Elementmitte bestimmt und dann anteilig auf die anliegenden Knoten verteilt. Ergibt im Allgemeinen die besten Werte. Nur im Randbereich treten Abweichungen in den Momenten auf.

• Verfahren 2:
  Die Momente werden in der Nachlaufrechnung an den Dreiecksknoten eines jeden Elements bestimmt. Der tatsächliche Wert an jedem Knoten ergibt sich aus einer Mittelung. Ergibt nur bei einfachen Systemen bessere Werte als Verfahren 1 (Randbereich).

Die Querkraftberechnung ist ein weiteres grundsätzliches Problem bei Finite-Element-Verfahren, da wegen der Ableitung der Momente eine weitere Aufrauhung des Funktionsverlaufs entsteht.

Die Qualität der berechneten Verschiebungen ist i.a. hervorragend. Wenn Sie sich nur für die Verschiebungen interessieren, müssen Sie sich um die vorstehenden Erläuterungen keine Gedanken machen.

Denken Sie weiterhin daran, dass alle Finite-Element-Methoden Näherungsverfahren sind. Die Qualität der Näherung steigt mit zunehmender Netzdichte. In der aktuellen Version können Systeme berechnet werden, die maximal 45000 Dreieckselemente und Knoten enthalten.